桁架的拓扑优化 - 问题

花点时间讲下我这个学期忙了写啥，这是第一篇，所以先讲讲花的功夫最多的吧。

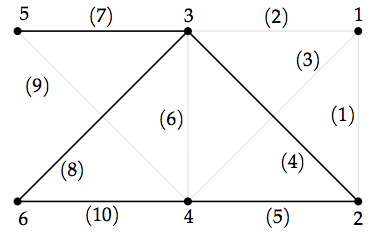
其实问题很简单，就是给定空间中节点，给定外力作用情况和固定端，目的是合理地连接这些节点设计出一个能够承载外力的结构。比如说楼上那个问题，平面中给定6个节点，在节点2上作用一个往下的外力，而节点5、6固定，我们想设计一个平面桁架来传递这个外力。

“合理地连接这些节点设计出一个能够承载外力的结构”这句话隐含了很多东西…“合理”是什么意思？这就需要我们去定义了。比如说我们寻找一个使用最少的材料（最少的体积或最少的杆长度总和）并满足应力限制（比如杆中的应力不能超过弹性极限）的结构，这就变成了一个数学上的最优化问题。其次，“结构”这个词意味着它是稳定的而不是个“机构”，但是我们可以看到不是随便连这个点就能产生个“结构的”…比如说下图，是一个有1个自由度的机构。

解决这个问题的第一步，同时也是目前所有想用科学的办法解决问题的第一步，就是用数学的语言去重新“表达”这个问题，也就是所谓的数学建模啦。然后我们经常可以发现可以用很多种不同的方式去表达同一个问题，表达的不同，之后进行求解时采用的方法也就不同，得到的答案也就不一定一样，如何去解释这些答案也是我们要做的事情（我们是谁？）

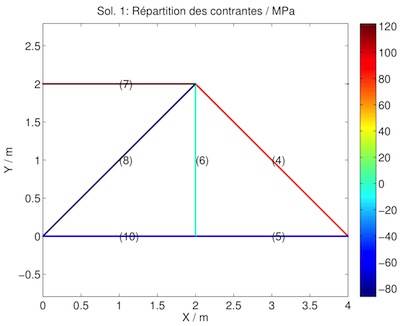
还要讲很多东西，所以在等大家睡着之前，先放上楼楼上那个问题（最小化体积，保证杆内应力不超过材料的弹性极限）的结果：

颜色代表杆中应力的大小，正值代表拉应力，负值代表压，采用 CPLEX 进行求解，差不多花了 0.03 秒计算出结果…在此再次惊叹下 CPLEX…

下次讲我们是如何数学建模的，再下次讲如何求解的。