你一生的故事
通过《攻壳机动队》知道了离线杂志1,内容很符合我的胃口:科学、技术、人文、哲学。上上周一期介绍了特德·蒋,一位华裔科幻小说家。大致看了下介绍觉得挺有意思,就立马在 Kindle 上买了它的小说集《你一生的故事》。这本小说集以其包含的第一个故事命名。一开始没有期望特别大,这很正常,因为没看完之前谁都不知道会第一次成为自己最喜欢的故事。这篇博文就试试惭愧地做一点微小的工作,介绍下这篇科幻小说。
关键字:科幻、对称、语言、认知、目的、因果、自由意志。
「三体」以其广阔的世界观以大见大,客体为整个宇宙;「你一生的故事」则以一次毫无”成果“的外星人访问以小见大,描述了一名语言学家 Louise 所经历的一系列故事。在学习外星语言过程中,她渐渐意识到生物个体的对称性与其语言系统的相互对应。小说的高潮起于一次与外星人偶然的科学交流。它们与人类不同的语言体系背后蕴含着它们对于世界的认知。作为第二语言,它深深影响了 Louise 对于人生的看法。在时间之书面前,一切的根源来自目的,因和果无需辗转相生,而自由意志只是幻想。从中,她看见了十个月后即将出生的金发小女孩一生的故事。
令我着迷的是作者对物理学原理的哲学探讨及其在人生认知上的衍生。篇幅不长,一小时即可读完。如果能更早一点遇到本书,我一定会把它刻进答辩论文,毕竟这个对自然最优美的阐述即是我的博士课题……
下面就说下本书所探讨的最小作用量原理,和作者从中进行的科幻衍生。
最小作用量原理
正如书中所说,最小作用量原理属于一种对物理现象的变分描述。这类变分原理广泛运用于物理学各类分支中:光学(书中所讲的费尔马原理)、固体力学(最小势能原理)、量子力学(薛定谔方程)等等。我的博士课题就是将最小作用量原理推广到了动态裂纹传播,见这里。
不同于其他变分原理,本书所探讨的最小作用量原理是动态的,即涉及了一个时间上的积分2,目的是描述物理现象随时间的演化。假定一个物理现象由一个时间的函数 \(t\mapsto u(t)\) 描述(可以是标量,矢量,甚至是空间场)。要真正从物理角度理解这个原理,就要明白最小作用量原理是如何一步步运用的:
- 给定这个物理现象的始末状态 \(u(0)\), \(u(T)\)。比如对于一个单摆,未知函数是单摆角度 \(\theta\),始末状态分别是一开始和最终的角度。
- 通过物理建模,我们为每一个可能发生的演化情况 \(u\) 都对应一个实数:作用量 \(u\mapsto\mathcal{A}(u)\)。对于单摆,作用量为动能减去重力势能在 \([0,T]\) 上的积分。
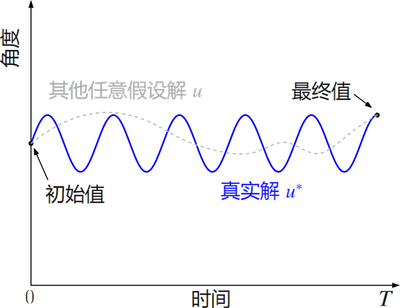
- 最小作用量原理断言,事实上客观真正发生的物理现象 \(u^*\),必然使得作用量取驻值。简单情况下,这将是(局部)最小值或最大值3。数学上,原理可以写为 \(\mathcal{A}'(u^*)=0\),即作用量的一阶函数导数,取在真实解 \(u^*\) 处,为零。通过这个原理,我们即可以推导出这个物理现象的演化方程。由于 \(u^*\) 通常取极值,使得作用量最大化或最小化,所以它也称作最优解。可以看到,要应用这个原理,必须考虑所有可能发生的时间上的演化情况 \(u\),然后寻找其中的最优解。正是由于这个数学和物理上 elegant 的变分结构,这个原理一直被很多理论家推崇(比如我导师,和我)。
排除一些数学上的细节,物理上这里的关键在于,要达到我们的目标——即预测出物理现象在时间 \(0\) 到 \(T\) 之间的演化,我们必须先知道或给定它的初始状态(这个没事)和最终状态——而这,却正是我们一开始所不知道的。我接下来就从物理和哲学的角度讨论这个问题。
目的论、因果关系
从物理建模的角度(比如我的博士),上面这个略哲学问题通常就忽略了。原因在于通过最小作用量原理我们可以推导出 \(\theta\) 的 Euler-Lagrange 微分方程:
\[\frac{\mathrm{d}^2\theta}{\mathrm{d}t^2}+\frac{g}{l}\sin\theta=0\]这个方程决定了在每一时间 \(t\) 单摆角度的加速度 \(\ddot{\theta}\)。如果知道 \(u\) 的初始状态(位置 \(\theta(0)\) 和速度 \(\dot{\theta}(0)\) 比如)就可以当作一个初始值问题 Initial Value Problem 并解析或数值求解得到 \(\theta\) 的演化,从而计算出其最终状态。这个初始值问题符合我们对物理学的实用需求:预测未来。它也符合我们对世界的认知:过去为因,未来为果;而这本身来源于时间之矢无法回到过去的事实。另一方面,从受力角度来看,当前受到的外力(因)将影响其将来的运动状态(果)。这个因果关系可以在上面的微分方程中看到。
当如果我们暂止忘记这个有点“作弊”的推导,我们必须严格根据上述 3 个步骤求解。从数学角度,可以把最小作用量原理看作一个边界值问题 Boundary Value Problem,因为解在定义域 \([0,T]\) 的两端被固定住了。正如上一节最后所述,这个问题没有实用意义。在现实生活中事实上我们无法运用最小作用量原理:第 1 步我们就跪下。从实用角度看,如果真的要寻找最小作用量原理的意义的话,那就是检测过去大自然有没有好好工作:假设现在时间为 \(t\),而 \(0<T<t\),即时间区间属于过去,那么我们就可以闲得无聊去检测真实发生的物理现象是不是真的是最优解。
现在抛去实用角度,纯粹从物理和哲学角度分析最小作用量原理本身,可以发现它不仅不存在因果关系,还有点“目的论”的倾向:在未来的最终状态已经确定的前提下,一个自然现象的演化必须是最优的。未来的状态(果)成为了过去系统演化的决定因素(因)。另一方面,不管它之间会怎么演化,它的目的肯定是达到之前的给定最终状态;它的目的肯定是比较所有可能的演化情况,然后寻找最佳的情况。这个问题就是小说着重探讨并科幻化的地方,见下节。
从物理角度,这个问题在维基百科和 StackExchange 上都有讨论,下面是一个解决方案,我不能说是我想出来的因为大致的想法我在其他地方也看到过。
最小作用量原理只是……一个原理。这个原理本身没有固定住最终状态,而是要你去确定系统的最终位置。在最初位置确定的情况下,原理只是说,如果最终位置是那里的话,那么系统的演化会是这样的。如果你对最终位置一无所知(很正常),那么你可以对最终位置任意取值:每取一个值,你就可以计算出对应这个最终位置的系统演化。接下来,我们可以注意到最小作用量原理并没有固定住系统的演化速度。如果初始速度 \(\dot{u}(0)\) 确定的话,那么我们可以在所有符合最小作用量原理的演化中寻找符合 \(\dot{u}(0)\) 的那个——这就是我们寻求的解。这个有点像数值求解中的 Shooting method。在解唯一、初始位置确定的情况下,初始速度可以与最终位置一一对应。所以其实最小作用量原理不存在目的论,也没有违背一般的因果关系。
科幻元素
在讲述最小作用量原理的时候,通常会讲涉及到的物理现象(如书中的折射光,或上面的单摆)进行拟人化修辞。大自然仿佛拥有了“神性”,它不仅得知道它的终极目的是什么,还必须在所有可能的路径中选择一条最优解。它仿佛失去了自由意志:为了达到目的,它只能看着自己慢慢走向那条最优的道路,现在做出的选择(施加的外力)无法再对未来产生影响。
本书则将这套思维运用到了七肢桶上。七肢桶的思维方式就是“目的论”式的:目的为先,然后在所有未来可能的决定中挑出最优解,然后进行所谓的“表演”或仪式。在这种思维方式下,因果和自由意志是个荒谬的概念,因为你无法违背自己的岁月之书,自己的“命运”。
表演:可以用这个词来描述你预先知道双方的对话,就像在舞台上演出……人类自发产生的、具有交流功能的一句句口语对话都变成了仪式,人人都在执行这个仪式,背诵自己的台词。(特德·蒋:你一生的故事)
使 Louise 理解到这一点的,正是因为它们的语言:一种没有方向性的纯二维书写系统。人类的书写语言完全是口语的再现,如果技术上存在一条很长的纸条的话,完全可以不需要进行二维式段落划分而把全书的内容线性地展示在带有方向的一维线段上。而这一切,都是源于我们和它们生物性外形上的区别:我们的身体有前后方向区分,而它们是完全对称的。本书中存在如下很新颖的类比:
| 人类 | 七肢桶 | |
|---|---|---|
| 书写系统/生物体型 | 方向性 | 没有方向性 |
| 世界因果关系 | 时间之矢(存在前因后果) | 可以随意前后翻阅岁月之书(不存在因果) |
| 个体思维方式 | 自由意志(未来可以通过过去改变) | 目的论(一切都是为了未来的表演) |
好玩的是,学习和掌握了七肢桶的语言之后,Louise 也渐渐有了它们的思维方式。
通过上一节自己的理解,我可以进行一些补充。由于目的成为了一个自己可以选择的自由度参数,所以可以把目的的选择看作是另外一种自由意志:
| 自由意志 | 人类 | 七肢桶 |
|---|---|---|
| 体现在 | 现在 | 目的 |
| 因果方向 | 现在(包括过去)作用到未来 | 未来作用到过去 |
| 自由选择次数 | 无数次(每时每刻) | 一次 |
| 最终状态 | 只存在一个最终结果 | 存在无限个可选择的最终目的 |
如果总结如上表格的话,你可以选择
- 人类的方式:你每时每刻都可以做出自由意志的决定,这些决定都会影响到今后自己的状态,但你必须要接受如下事实:你只有一个最终终点。最终终点的好坏,取决于你之前做出的选择。
- 七肢桶的方式:你可以自由选择你想要的结局,你可以随便选,但只有一次机会。选择好之后,你失去了自由意志自由选择的权利,你只能看着自己慢慢表演着走向自己想要的那个结局。
你想要哪一个?

留下评论