一个力学小知识

这篇博文介绍一个日常生活中可以简单验证的力学小知识，叫做 Intermediate axis theorem。设某刚体的惯性主轴为 \((\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3)\)，相对应的转动惯量为 \(I_1\geq I_2\geq I_3\)。这个定理说，在没有外力矩的情况下，刚体关于第二主轴 \(\mathbf{e}_2\) 的自转是不稳定的。

现象

这个定理其实很好用实验证明，拿出各位的手机就行了¹。见下图，围绕着手机的中心，可以有三种旋转方式。

1. 围绕着 \(\mathbf{e}_1\)，在手机屏幕的平面中旋转。
2. 围绕着 \(\mathbf{e}_2\)，手机的上半部分和下半部分线速度相反。
3. 围绕着 \(\mathbf{e}_3\)，手机的左半部分和右半部分线速度相反。

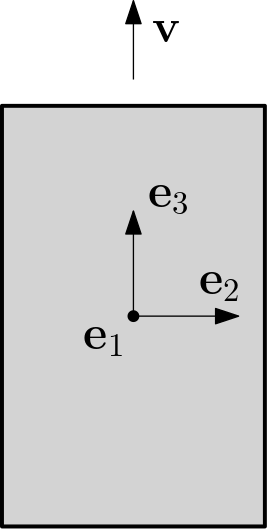
为了去除施加在手机上的外力矩，你可以在给予初始旋转角速度的同时，把手机往上抛。手机在上升和下降过程中，尽管有重力作用，但不会收到外力矩。

通过数值模拟，我得到了如下仿真结果，从左到右分别对应上述三种旋转方式。

1. 第一种情况手机的自转是稳定的：手机在平面中的旋转是匀速，而且旋转轴本身几乎没有任何变化。
2. 第二种自转是不稳定的：手机没有一个固定的旋转方式，围绕着其他轴的旋转也参与了进来。
3. 第三种自转是稳定的：尽管肉眼可见旋转轴本身有稍许的变化，但主旋转仍然是围绕着初始的 \(\mathbf{e}_3\) 轴。

如果实在不想弄坏自己的手机或者书的话，也可以看看这个 YouTube 视频。

重温刚体力学

说解释，其实还是需要用到牛顿力学的知识和一些数学工具。研究力学问题，第一步是描述物体的运动，即运动学。一个刚体在某一瞬间的运动可以用两个三维矢量来刻画。

1. 质心 \(\mathbf{x}_\mathrm{C}\) 的速度 \(\mathbf{v}_\mathrm{C}=(v_x, v_y, v_z)\)。在材料密度均匀的情况下，一个刚体的质心、即质量中心，等于几何中心。
2. 围绕着质心的角速度 \(\Omega=(\omega_x, \omega_y, \omega_z)\)，方向指向此刻的旋转方向，大小 magnitude 为此刻旋转的速度，单位是 rad / s。

刚体上任意一点 \(\mathbf{x}\) 的速度 \(\mathbf{v}\) 可以由 \(\mathbf{v}_\mathrm{C}\) 和 \(\Omega\) 如下公式计算而得，即质心的运动加上旋转得到合成速度。

\[\mathbf{v}=\mathbf{v}_\mathrm{C} + \Omega\times(\mathbf{x}-\mathbf{x}_\mathrm{C}).\]

在没有外力的情况下，牛顿力学应用到刚体上有如下两个结论

• 线动量守恒

\[m\mathbf{a}=m\ddot{\mathbf{x}}_\mathrm{C}=\mathbf{0}.\]

• 角动量守恒

\[\mathbf{I}\dot{\Omega}+\Omega\times(\mathbf{I}\Omega)=\mathbf{0}.\]

其中 \(\mathbf{I}\) 为表述在随着刚体一起旋转的坐标系中的惯性张量。通常这个与刚体一起旋转的坐标系就取为刚体的旋转主轴坐标系，可得到 \(\mathbf{I}=\mathrm{diag}(I_1, I_2, I_3)\)。在这个主轴坐标系下，角动量守恒可以写成

\[\begin{aligned} & I_1\dot{\omega}_1 = (I_3-I_2)\omega_2\omega_3 \\ & I_2\dot{\omega}_2 = (I_1-I_3)\omega_3\omega_1 \\ & I_3\dot{\omega}_3 = (I_2-I_1)\omega_1\omega_2 \end{aligned}\]

这里的 \((\omega_1, \omega_2, \omega_3)\) 均为刚体在此刻相对于主轴的旋转角速度。下面来根据 \((\omega_1, \omega_2, \omega_3)\) 的大小来分析旋转的稳定性。

刚体围绕第一主轴自转

在这个情况下假设 \(\omega_1\gg 0\)，\(\omega_2\approx 0\), \(\omega_3\approx 0\)。根据上述第一条公式，刚体关于第一主轴的角速度将几乎保持不变。

\[\dot{\omega}_1\approx 0.\]

对第二条公式两边对时间求导，得到

\[I_2\ddot{\omega}_2 = (I_1-I_3)\dot{\omega}_3\omega_1.\]

将第三条公式的 \(\dot{\omega}_3\) 带入，得到

\[I_2I_3\ddot{\omega}_2 = (I_1-I_3)(I_2-I_1)\omega_1^2\omega_2.\]

由于 \(I_1\geq I_2\geq I_3\)，即 \((I_1-I_3)(I_2-I_1)\leq 0\), 上述公式对时间积分后是时间的三角函数，于是得到关键结论：关于第二主轴的角速度是时间的周期函数，且振幅不会无限放大。

同理，可以得到刚体围绕第二和第三主轴的旋转是稳定的，即保持在几乎为零的旋转速度。

刚体围绕第三主轴自转

类似上述推理，可以得出刚体围绕第一和第二主轴的旋转是稳定的。

刚体围绕第二主轴自转

这个时候，可以得到

\[\begin{aligned} & I_1I_3\ddot{\omega}_1 = (I_2-I_3)(I_1-I_2)\omega_2^2\omega_1 \\ & I_1I_3\ddot{\omega}_3 = (I_2-I_3)(I_1-I_2)\omega_2^2\omega_3. \end{aligned}\]

此时，可以发现 \((I_2-I_3)(I_1-I_2)\geq 0\)，那么不管 \(\omega_1\) 和 \(\omega_3\) 初始值多小，也会（一开始）呈指数变大，所以这时刚体围绕第一和第三主轴的旋转是不稳定的。这就解释了一开始的现象。

如何对角速度积分

现在说一个后话，是我研究这个问题的时候遇到的问题。前面算了那么多，最终得到的是刚体的角速度矢量关于时间的函数，并不是刚体的旋转关于时间的函数。为了得到每一时刻刚体具体的姿势，必须对角速度矢量进行“积分”。之所以“积分”一词用了引号，是因为刚体的旋转并不是一个矢量，不可能对角速度矢量的每个分量直接积分就可得到。

通常来说刚体的旋转可以由一个旋转矩阵 \(\mathbf{R}\) 来描述。假设坐标系原点不动，一个关于坐标系原点方位是 \(\mathbf{x}\) 的质点在旋转后将位于

\[\mathbf{x}'=\mathbf{R}\mathbf{x}.\]

另外一个更加简洁和数值稳定的描述刚体旋转的方式是通过四元数。参考 How to Integrate Quaternions 这篇文章，得到四元数和角速度的关系

\[\dot{\mathbf{q}}=\frac{1}{2}\mathbf{q}\otimes\Omega,\]

其中 \(\otimes\) 为四元数的乘法，而 \(\Omega\) 为刚体关于主轴（而不是关于固定的实验坐标系）的角速度。通过 scipy.integrate.solve_ivp 可以很容易得到积分结果。

本博文的所有数值仿真均可由这个 Jupyter notebook 生成。

1. 如果你把手机摔坏的话，也别忘了拍张类似这样的照片，用来研究裂纹的动态传播。 ↩